A cinema has n rows, numbered from 1 to n. There are 10 seats in each row, labelled from 1 to n as shown above.
We are given an array occupiedSeats containing the number of seats already occupied , example occupiedSeats[I] = [3,8] means the seat located in row 3 and labelled 8 is already occupied.
we need to return the maximum number of 4 person groups that can be assigned to the cinema seats. A 4 person group occupies 4 adjacent seats in one single row. Seats across an aisle (like [3,3] and [3,4]) are not considered to be adjacent, but in an exceptional case on which an aisle split a 4 person group, in that case, the aisle split the group in the middle, i.e two people on each side
Example 1:
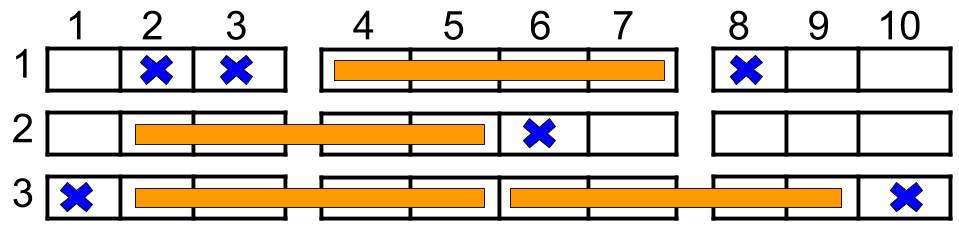
Input: n=3, occupiedSeats = [[1,2],[1,3],[1,8],[2,6],[3,1],[3,10]]
Output: 4
constraints :
1<=n<=(10^9)
occupiedSeats.size()<=(10^4)
Solution:
First of all the first thing that comes to mind is checking for every row the number of groups that are possible to assign, but due to the large of n this will give time limit exceed, so we can not do this.
Now we have to iterate over occupiedSeats now we sort occupiedSeats based on the first element of each row. now we store all elements of a single row in another vector of sets called reserved, where every set in reserved holds those the occupied column numbers for each row.
After this, we iterate over each row of reserved and count the number of groups.
Now their will 3 cases
Case 1: Seats 4,5,6,7,8,9 are not occupied, in this case we can form 2 groups.
Case 2: Either the seats 2,3,4,5 are not occupied or the seats 6,7,8,9 are not occupied, in this case we can only form 1 group.
Case 3: Seats 4,5,6,7 are not occupied, in this case we can form 1 group.
Note: For the rows in which no seats are occupied for each of such rows also 2 groups can be formed , so we add these groups also in the end.
Code:
bool mycomp(const vector<int>& v1,const vector<int>& v2)
{
return v1[0]<v2[0];
}
int maxNumberOfGroups(int n, vector<vector<int>>& occupiedSeats) {
int maxGroups=0;
sort(occupiedSeats.begin(),occupiedSeats.end(),mycomp);
int x=0;
vector<set<int>> reserved;
set<int> s;
reserved.push_back(s);
reserved[0].insert(occupiedSeats[0][1]);
for(int i=1;i<occupiedSeats.size();i++)
{
if(occupiedSeats[i][0]!=occupiedSeats[i-1][0])
{
x++;
set<int> s2;
s2.insert(occupiedSeats[i][1]);
reserved.push_back(s2);
}
else
{
reserved[x].insert(occupiedSeats[i][1]);
}
}
for(int i=0;i<reserved.size();i++)
{
if(reserved[i].find(2)==reserved[i].end()&&reserved[i].find(3)==reserved[i].end()&&reserved[i].find(4)==reserved[i].end()&&reserved[i].find(5)==reserved[i].end()&&reserved[i].find(6)==reserved[i].end()&&reserved[i].find(7)==reserved[i].end()&&reserved[i].find(8)==reserved[i].end()&&reserved[i].find(9)==reserved[i].end()){
//cout<<"a";
maxGroups+=2;
continue;
}
else if((reserved[i].find(2)==reserved[i].end()&&reserved[i].find(3)==reserved[i].end()&&reserved[i].find(4)==reserved[i].end()&&reserved[i].find(5)==reserved[i].end())||(reserved[i].find(6)==reserved[i].end()&&reserved[i].find(7)==reserved[i].end()&&reserved[i].find(8)==reserved[i].end()&&reserved[i].find(9)==reserved[i].end())){
maxGroups++;
continue;
}
else if(reserved[i].find(4)==reserved[i].end()&&reserved[i].find(5)==reserved[i].end()&&reserved[i].find(6)==reserved[i].end()&&reserved[i].find(7)==reserved[i].end()){
maxGroups++;
continue;
}
}
return maxGroups+2*(n-reserved.size());
}



If you have any doubts or any new insights, please share ConversionConversion EmoticonEmoticon